Většina „důkazů“ o údajném podvodu během amerických prezidentských voleb byla již soudy smetena nebo byly vyvráceny americkými fact-checkery. Někteří lidé se proto obrací i na matematiku jako na vědu, která má dokázat, že Joe Biden podváděl při nedávných volbách. Řeč je o tzv. Benfordově zákoně.
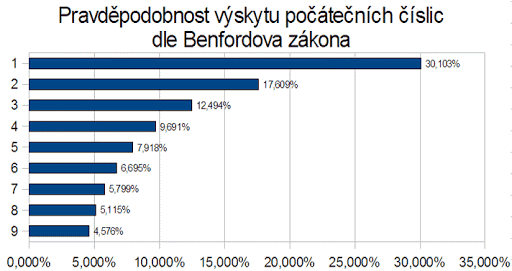
O co jde? Benfordův zákon je matematický zákon, který říká, že v mnoha souborech přirozených dat (ale ne ve všech) začínají čísla mnohem častěji číslicí 1 než jinou číslicí. Zhruba 30 % čísel začíná jedničkou. Čím vyšší počáteční číslice je, tím méně pravděpodobně se vyskytuje na začátku čísel. Ve skupině čísel reprezentujících reálné hodnoty čehokoli je asi 30% pravděpodobnost, že první číslovkou bude jednička. Dále pak 17,6 % čísel bude začínat dvojkou, 12,5 % trojkou a jen 4,57 % devítkou. To znamená, že z 1000 čísel v průměru 300 bude začínat jedničkou, 176 dvojkou a pouze 46 bude mít na prvním místě devítku. Nejde o žádný matematický trik, ale o skutečný přírodní zákon, jímž se řídí soubory jakýchkoli přirozených dat bez ohledu na jejich podstatu nebo fyzikální jednotky.
Matematici a amatérští matematici se snaží na základě tohoto zákona dokázat, že v některých okrscích a okresech se výsledky Joe Bidena odchylují od tohoto matematického zákona. Příkladem může být Milwaukee nebo i jiné okresy. V českém prostředí s touto metodou pracuje například Jan Červenka, Pavel Matocha nebo Jindřich Rajchl.
Ve skutečnosti koalice pro akademický a digitální výzkum Election Integrity Partnership varovala před závěrem, že odchylka od Benfordova zákona je důkazem volebních podvodů. Důvodem je, že jednotlivé okresy, které porovnáváme nejsou ani přibližně stejně velké. Theodore P. Hill, emeritní profesor matematiky na Georgia Tech v Atlantě zdůraznit, že Benfordův zákon nelze použít k prokázání podvodu.
Vyvrácení se velmi podrobně věnuje agentura Reuters.
A také toto video: